AC-LIO: Towards Asymptotic Compensation for Distortion in LiDAR-Inertial Odometry via Selective Intra-Frame Smoothing
Tianxiang Zhang
1,3
Xuanxuan Zhang
1
,*
Wenlei Fan
1
Xin Xia
2
Huai Yu
1
Lin Wang
3
You Li
1
1 Wuhan University
,
2 University of Michigan-Dearborn
,
3 Nanyang Technological University
(
* : Corresponding Author
)
Abstract
🔸Existing LiDAR-Inertial Odometry (LIO) methods typically utilize the prior trajectory derived from the IMU integration to compensate for the motion distortion within LiDAR frames. However, discrepancies between the prior and true trajectory can lead to residual motion distortions that compromise the consistency of LiDAR frame with its corresponding geometric environment. This imbalance may result in pointcloud registration becoming trapped in local optima, thereby exacerbating drift during long-term and large-scale localization.
🔸To this end, we propose a novel LIO framework with selective intra-frame smoothing dubbed AC-LIO. Our core idea is to asymptotically backpropagate current update term and compensate for residual motion distortion under the guidance of convergence criteria, aiming to improve the accuracy of discrete-state LIO system with minimal computational increase.
🔸Extensive experiments demonstrate that our AC-LIO framework further enhances odometry accuracy compared to prior arts, with about 30.4% reduction in average RMSE over the second best result, leading to marked improvements in the accuracy of long-term and large-scale localization and mapping.
🔸To this end, we propose a novel LIO framework with selective intra-frame smoothing dubbed AC-LIO. Our core idea is to asymptotically backpropagate current update term and compensate for residual motion distortion under the guidance of convergence criteria, aiming to improve the accuracy of discrete-state LIO system with minimal computational increase.
🔸Extensive experiments demonstrate that our AC-LIO framework further enhances odometry accuracy compared to prior arts, with about 30.4% reduction in average RMSE over the second best result, leading to marked improvements in the accuracy of long-term and large-scale localization and mapping.
(I) Accuracy and Criteria Validity Evaluation
(II) Principal Comparison
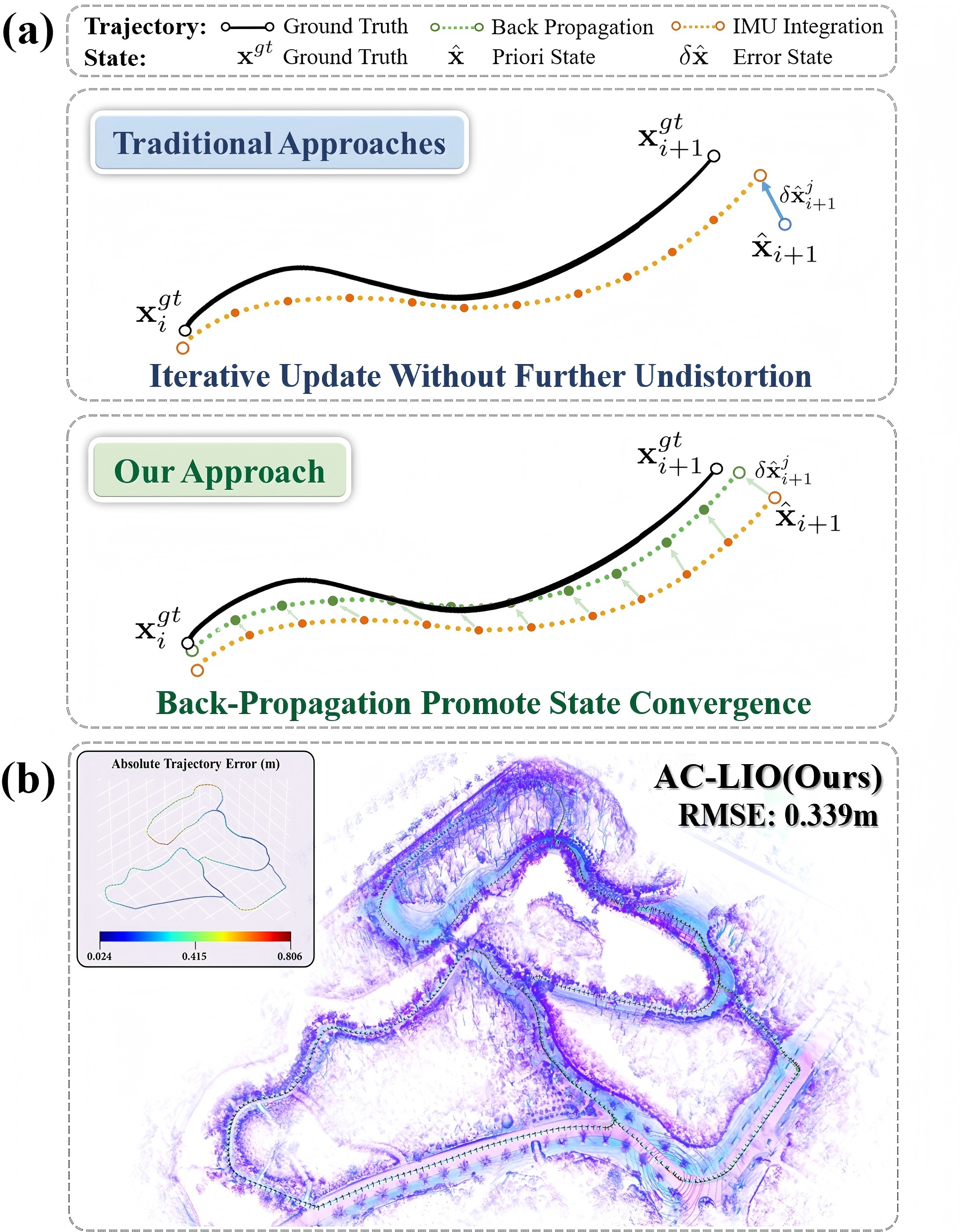
(a) A principal comparison of our AC-LIO with traditional approaches. Conventional LIO typically considers an initial distortion compensation via IMU, yet the residual motion distortion may prevent the registration from further convergence. Our AC-LIO employs a selective intra-frame smoothing strategy to asymptotically backpropagate and compensate for residual distortion.
(b) Large scale localization and mapping result of BotanicGarden dataset. We achieve better accuracy performance than other benchmark frameworks on its sequence Garden_1008 with VLP16 LiDAR.
(b) Large scale localization and mapping result of BotanicGarden dataset. We achieve better accuracy performance than other benchmark frameworks on its sequence Garden_1008 with VLP16 LiDAR.
(III) System Overview
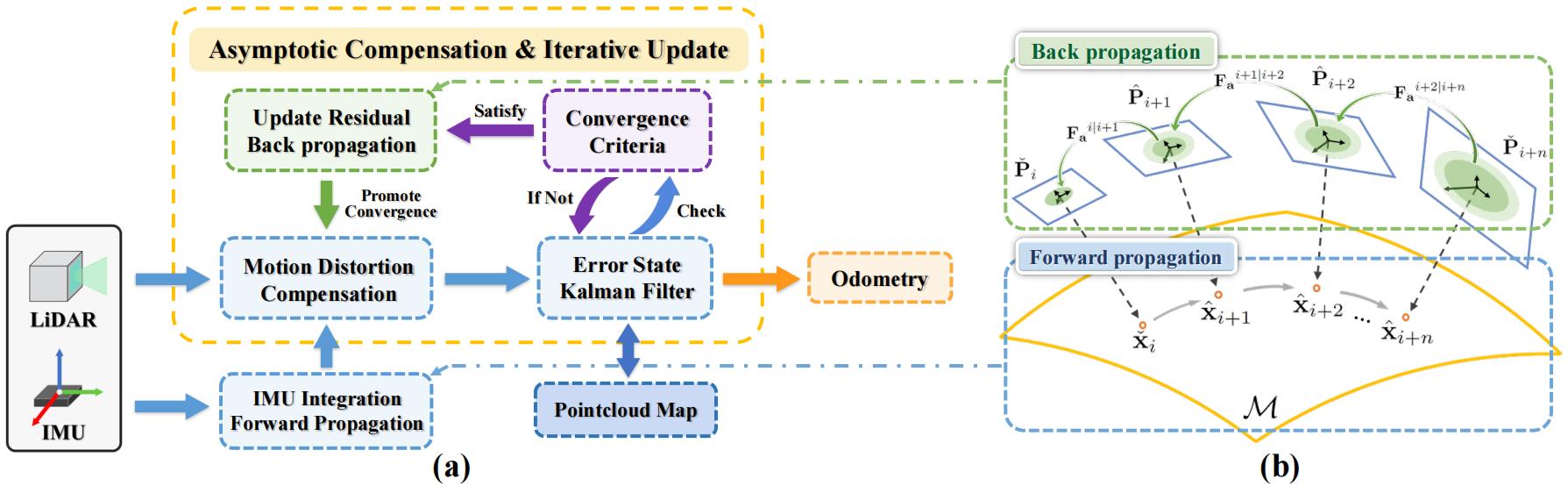
(a) The system overview of our AC-LIO framework. During iterative ESKF, the back propagation and asymptotic compensation for pointcloud distortion are conducted based on the convergence criteria.
(b) The on-manifold propagation. The blue shows the forward propagation of IMU integration. The green indicates the backward recursion of the update term according to the propagation matrix and noise relation.
(b) The on-manifold propagation. The blue shows the forward propagation of IMU integration. The green indicates the backward recursion of the update term according to the propagation matrix and noise relation.